Hexo
0%

MAR

发表于 更新于 分类于

0. 前言

出发点 Multi-label 很强，效果的确好，就是论文看得有点头晕，有些公式自己之前从来没见过，并且有些公式的出发点没有实验证明。

这篇论文是腾讯的，今年腾讯优图实验室25篇、腾讯AILab33篇共计55篇论文被 CVPR 2019 录取。

1. Introduction

这是篇跨数据集的行人重识别，source 是 MSMT，target 是 Market 和 Duke。

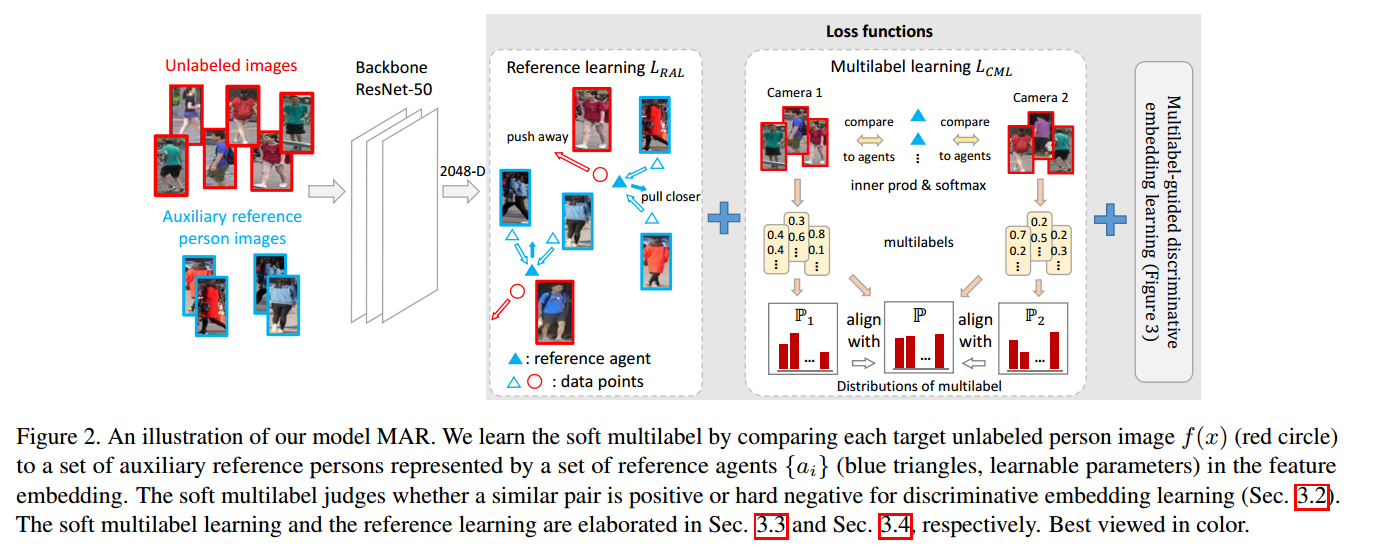
作者针对跨数据集行人重识别没有标签问题，提出四个工作：

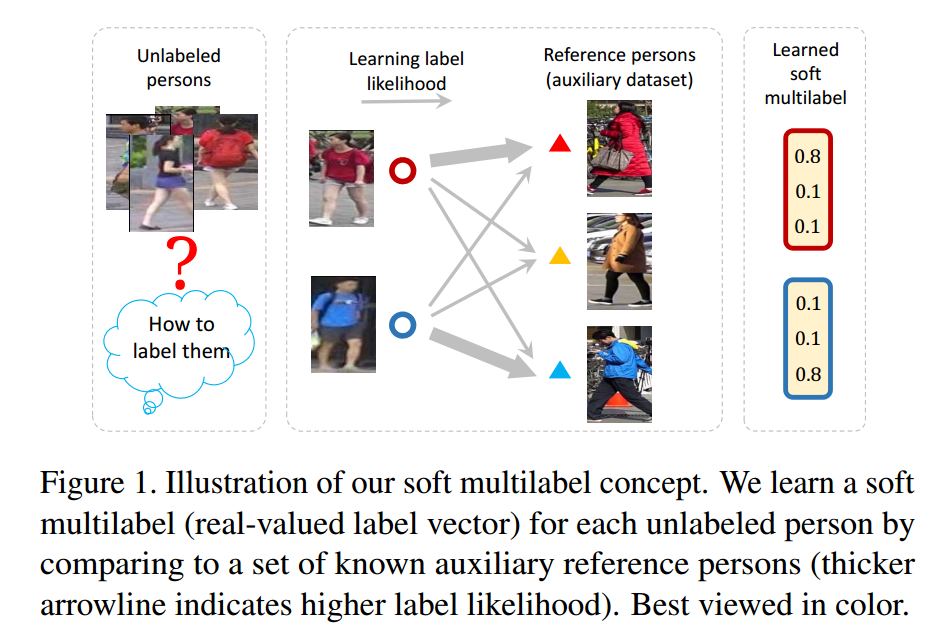
  1. soft multilabel learning, 示例如下图
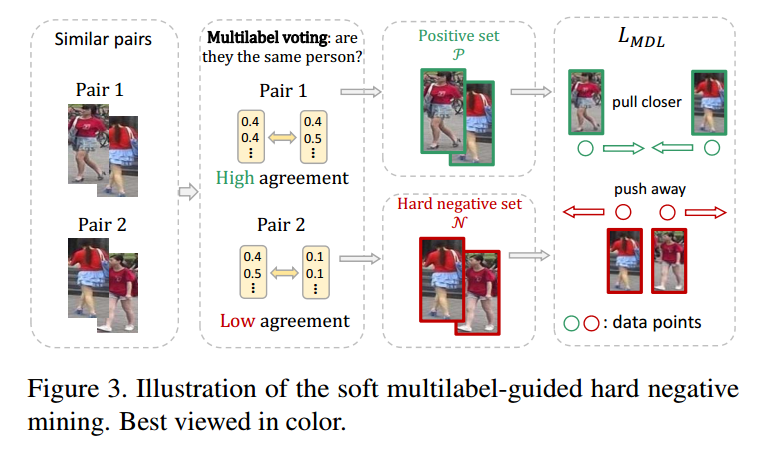
  2. soft multilabel-guided hard negative mining
  3. cross-view consistent soft multi-label learning
  4. reference agent learning
  1. 用分类结果作为图片的真值，即 soft multilabel
  2. 确定正负样本：特征相似但是 soft multilabel 不相似的作为负样本，特征相似且 soft multilabel 相似的作为正样本
  3. 跨摄像头的一致性，摄像头同一数据集下，应该是不管哪个摄像头下，得到的 soft multilabel 的分布是近似的，
  4. reference agent 应该满足：有标签数据集中，和 agent 同类别的图片得到的特征应该和 agent 相似，不同类别的图片得到的特征应该不相似，在无标签数据集中，图片得到的特征和 agent 应该不相似。

这几个点感觉完全没有联系啊，作者是咋想到的并放在一起的呢？

剩下的三个创新点后面依次阐述，其理解还是有点费劲的。

注:

  • 本论文中的 auxiliary dataset 等价于 source dataset
  • agent 是一个单独的 classx2048 维的数据，代码中是直接调用的 fc.weight。

2. Deep Soft Multilabel Reference Learning

2.1 Problem formulation and Overview

符号 含义
$X=\lbrace xi \rbrace{i=1}^{N_u}$ 没有标签的数据集，$N_u$张图片
$Z=\lbrace zi, w_i \rbrace{i=1}^{N_a}, \text{where }w_i=1,2,…, N_p$ 有标签的数据集 auxiliary，$z_i$表示图片，$w_i$表示 label，$N_a$ 张图片，$N_p$个人，有标签数据集和无标签数据集人物没有重叠
$f(\cdot)$ discriminative deep feature embedding，应该是特征提取模型，即 $f(x)$，满足 $\parallel f(\cdot) \parallel_2=1$
$\lbrace ai \rbrace{i=1}^{N_p}$ reference person feature, $\parallel a_i \parallel_2=1$
$y=l(f(x),\lbrace ai \rbrace{i=1}^{N_p})\in R^{N_p}$ soft multilabel function $l(\cdot)$, where $y=(y^{(1)}, y^{(2)}, …, y^{(N_p)})$, $\sum_i^{N_p} y^{(i)}=1, y^{(i)}\in [0, 1]$

一共有两个内容需要学习: $f(\cdot)$, $\lbrace ai \rbrace{i=1}^{N_p}$

2.2 Soft multilabel-guided hard negative mining

大哥，你的上下标能不能提前说清楚啊[捂脸]，算了算了，腾讯的，惹不起惹不起。

定义 soft multilabel function:

也就是说，用 $f(x)$ 去依次点乘 $a_k$， 然后用一个 softmax。

按照这个公式来说的话，是在特征空间上做的操作，有点类似 ECN 中的预测概率，越相似，值越大，而不是通过分类器预测概率。

代码中有温度T。

假设：如果一对样本 $x_i, x_j$ 有很高的特征相似性, 即 $f(x_i)^Tf(x_j)$，称之为相似样本。如果这对相似样本的其他特性也相似，则大概率为一对正样本，如果其他特性不相似，则大概率为一个难负样本 hard negative pair。

注：这里并没有实验证明一对 hard negative pair 的其他特性（主要指下文提到的 soft multilabel agreement）大概率不相似。所以表示存疑其假设的正确性。又想了想，在难采样三元组损失中，hard negative pair 就是指特征相似但是 label 不同的样本，positive pair 指 label 相同的样本的，easy positive pair 指 label 相同特征相似的样本，hard positive pair 指 label 相同特征不相似的样本，这样的话可以把 soft multilabel 看成样本的 label 的话，也是可以说得通的。

引理1：其他特性的相似性：作者选用 soft multilabel 作为其他特性，soft multilabel agreement $A(\cdot, \cdot)$ 表示作为其他特性的相似性。定义为

越相似，值越大。最后一个等号通过画图很容易求得，就不解释了。Question: 这里的相似性定义成了向量之间的一范，没有定义成熟悉的点积，暂时不知道原因。

引理2： hard negative pair：对于无标签数据集 $X$ 的所有样本对 $M=N_u\times (N_u-1)/2$，设置比例 $p$，取 $pM$ 个特征最相似的样本对，即 $\hat{M}=\lbrace (i,j)|f(x_i)^T f(x_j)\ge S\rbrace, \parallel \hat{M} \parallel=pM$, 其中 $S$ 表示 $pM$ 个特征最相似样本对的阈值，动态变化，不是很重要的，重要的是取 $pM$个样本对。然后根据 label 的相似性将这些样本对划分为 positive set $P$ and hard negative set $N$，即

其中 $T$ 表示 soft multilabel agreement 的阈值。会更新。

loss：soft Multilabel-guided Discriminative embedding Learning:

where,

so,

Question: 这是个啥公式啊，都没有见过类似的公式，作者也没有给出解释。

此时固定 agent $\lbrace ai \rbrace{i=1}^{N_p}$ ，学习 $f(\cdot)$.

实际训练时，$M=M{batch}=N{batch}\times (N_{batch}-1)/2$

2.3 Cross-view consistent soft multilabel learning

因为行人重识别要求跨摄像头识别，所以考虑到行人的分布应该与摄像头无关。

Loss:

其中，$P(y)$ 表示数据集 $X$ 的 soft multilabel 分布，$P_v(y)$ 表示数据集 $X$ 在摄像头 $v$ 的 soft multilabel 分布，$d(\cdot, \cdot)$ 表示分布的距离，可以是 KL divergence 或者 Wasserstein distance.因为实际观察到服从 log-normal 分布，所以采取 simplified 2-Wasserstein distance。

其中，$\mu/\sigma$表示总体数据集的 log-soft multilabel 的均值和方差，$\mu_v/\sigma_v$表示总体数据集在摄像头$v$的 log-soft multilabel 的均值和方差.
Question: 这个公式又是咋推出来的，这是妥妥地写出来也看不懂系列。

此时固定 agent $\lbrace ai \rbrace{i=1}^{N_p}$ ，学习 $f(\cdot)$.

2.4 Reference agent Learning

考虑到 referentce agent 需要与 soft multilabel function $l(\cdot, \cdot)$ 有关，因此得到损失函数

其中，$z_k$ 表示有标签数据集 $Z$ 中标签为 $w_k$ 的第 $k$ 张图片。

这里可以理解成 $z_k$ 的预测概率和真实概率的交叉熵损失。这个损失函数不仅训练 $a_i$ 更接近第i个人的所有图片的特征，也训练 feature embedding $f$，使 $l(\cdot, \cdot)$ 得到的标签更具有表示同一个人的能力，符合 soft multilabel-guided hard negative mining 的假设：特征相似，但是 soft multilabel 不相似的为 hard negative mining。

这个公式更新的是 $f$ 和 agent $a_i$.

注：该论文中的公式其实按照从广义的定义到实际的应用的具体化过程，所以刚开始才会感觉有点乱，公式里面的字符也会一变再变，其实是从理论的公式到具体化实际代码的过程。

Joint embedding learning for reference comparability: 为了更好地提高 soft multilabel function 表示无标签数据集图片的正确性，提出 Joint embedding learning for reference comparability，为了修正 domain shift，利用无标签数据集 $f(x)$ 和 $a_i$ 肯定不是一对，提出 loss:

其中，其目的是为了保证$a_i$所表示的有标签数据集中的同一id的图片和$a_i$特征相似，$a_i$和所有无标签数据集中的图片特征都不相似。 $M_i=\lbrace j| \parallel a_i-f(x_j) \parallel_2^2 < m \rbrace$，表示对第 $i$ 个 agent $a_i$ 而言，特征最为相似 ($\parallel a_i-f(x_j) \parallel_2^2=2(1-a_i^Tf(x_j))$, 越相似，值越小) 的无标签数据集中的图片，按照作者推荐的论文 44:Normface: l2 hypersphere embedding for face verification，建议 $m=1$。

此时固定 agent $\lbrace ai \rbrace{i=1}^{N_p}$ ，学习 $f(\cdot)$.

对 $L{RJ}$ 根据代码再次做出解释，$L{RJ}$ 的目的是学习更好的特征提取器 $f$，使有标签数据集提取出的特征与同类别的 agent 的特征相似，与不同类别的agent不相似，无标签数据集提取出的特征与 agent 都不相似，有点三元组损失的意思。此时的 $ai$ 是常量，不进行反向求导的。其二，对于任意一个 agent $a_i$，有标签数据集中，label 等于 $i$ 的图片视为正样本，其他图片视为负样本，对于无标签数据集，则直接视为 $a_i$ 的负样本。具体来说，就是对每一张有标签数据集的图片，$a{label}$ 为正， 其余 $a_i$ 为负，对于每一张无标签数据集的图片，$a_i$ 都为负。

所以总的 reference agent learning loss为:

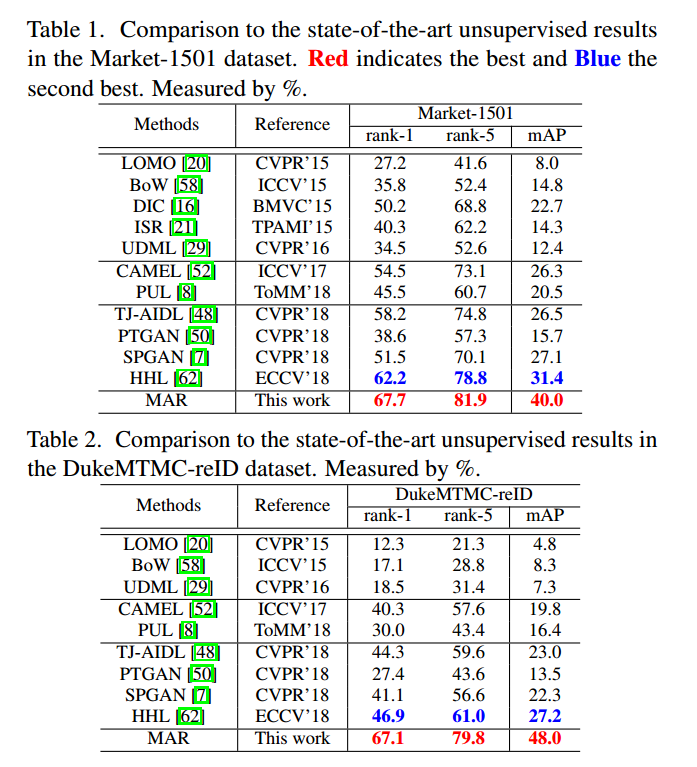
2.5.1 Model training and testing

3. Experiments

MSMT17 为辅助数据集， Market-1501、Duke 为无标签数据集。

备注: 论文中的 agent 其实并不是之前以为通过图片输入模型得到的特征求出来的，而是 ResNet-50 的 fc.weight(classx2048) ，也就是分类器的分类向量。和 ECN 论文中的使用方法有很大的不同吧。在 ECN 中，使用的就是图片输入模型得到的特征，可能是因为 ECN 中一张图片对应一个特征，而本论文中是多个图片对应一个特征。

4. code

4.1 Logger

两种logger

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 第一种：定义简单，使用繁琐
# 定义
import time
def time_string():
    ISOTIMEFORMAT = '%Y-%m-%d %X'
    string = '[{}]'.format(time.strftime(ISOTIMEFORMAT, time.localtime(time.time())))
    return string

class Logger(object):
    def __init__(self, save_path):
        if not os.path.isdir(save_path):
            os.makedirs(save_path)
        self.file = open(os.path.join(save_path, 'log_{}.txt'.format(time_string())), 'w')
        self.print_log("python version : {}".format(sys.version.replace('\n', ' ')))
        self.print_log("torch  version : {}".format(torch.__version__))

    def print_log(self, string):
        self.file.write("{}\n".format(string))
        self.file.flush()
        print(string)
# 使用
logger = Logger(args.save_path)
logger.print_log("=> loading checkpoint '{}'".format(load_path))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# 第二种，定义繁琐，使用简单，重定向
# 推荐用这种
# 定义
# .\logging.py
from __future__ import absolute_import
import os
import sys
import errno

def mkdir_if_missing(dir_path):
    try:
        os.makedirs(dir_path)
    except OSError as e:
        if e.errno != errno.EEXIST:
            raise

class Logger(object):
    def __init__(self, fpath=None):
        self.console = sys.stdout
        self.file = None
        if fpath is not None:
            mkdir_if_missing(os.path.dirname(fpath))
            self.file = open(fpath, 'w')

    def __del__(self):
        self.close()

    def __enter__(self):
        pass

    def __exit__(self, *args):
        self.close()

    def write(self, msg):
        self.console.write(msg)
        if self.file is not None:
            self.file.write(msg)

    def flush(self):
        self.console.flush()
        if self.file is not None:
            self.file.flush()
            os.fsync(self.file.fileno())

    def close(self):
        self.console.close()
        if self.file is not None:
            self.file.close()
# 使用
import sys
import os.path as osp
sys.stdout = Logger(osp.join(args.logs_dir, 'log.txt'))
print(args)

4.2 model

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class ResNet(nn.Module):
    def forward(self, x):
        # 3x384x128
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.maxpool(x)

        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        feature_maps = self.layer4(x)
        # 2048x12x4
        x = self.avgpool(feature_maps)
        x = x.view(x.size(0), -1)
        # bx2048
        # renorm 使每一行的向量的2范进行了截断处理
        # 使之变成[0,1e-5]，再线性变成[0,1]
        # 这里的renorm可以暂时理解成进行了二范处理，
        feature = x.renorm(2, 0, 1e-5).mul(1e5)
        # bx2048
        w = self.fc.weight
        # 注: 这个self.fc.weight(classx2048)就是论文中的agent
        ww = w.renorm(2, 0, 1e-5).mul(1e5)
        sim = feature.mm(ww.t())
        # sim: bxclass
        # feature(f): bx2048, sim(y): bxclass, feature_maps: 2048x12x4
        return feature, sim, feature_maps

4.3 optim

1
2
3
bn_params, other_params = partition_params(self.net, 'bn')
self.optimizer = torch.optim.SGD([{'params': bn_params, 'weight_decay': 0},
                                  {'params': other_params}], lr=args.lr, momentum=0.9, weight_decay=args.wd)

4.4 trainer/init_losses

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
class ReidTrainer(Trainer):
    def __init__(self, args, logger):
        self.al_loss = nn.CrossEntropyLoss().cuda()
        self.rj_loss = JointLoss(args.margin).cuda()
        self.cml_loss = MultilabelLoss(args.batch_size).cuda()  # L_CML
        self.mdl_loss = DiscriminativeLoss(args.mining_ratio).cuda() # L_MDL
        self.net = resnet50(pretrained=False, num_classes=self.args.num_classes)
        self.multilabel_memory = torch.zeros(N_target_samples, 4101)
    def init_losses(self, target_loader):
        self.logger.print_log('initializing centers/threshold ...')
        if os.path.isfile(self.args.ml_path):
            (multilabels, views, pairwise_agreements) = torch.load(self.args.ml_path)
            self.logger.print_log('loaded ml from {}'.format(self.args.ml_path))
        else:
            self.logger.print_log('not found {}. computing ml...'.format(self.args.ml_path))
            sim, _, views = extract_features(target_loader, self.net, index_feature=1, return_numpy=False)
            # sim: bxclass, views: bx1
            multilabels = F.softmax(sim * self.args.scala_ce, dim=1)
            # multilabels: bxclass 这里应该对于soft multilabel funtion得到的结果y^{(k)}
            # Question: sim*self.args.scala_ce 是什么意思
            ml_np = multilabels.cpu().numpy()
            pairwise_agreements = 1 - pdist(ml_np, 'minkowski', p=1)/2
            # pairwise_agreements: soft multilabel agreement A(.,.) 公式2
        log_multilabels = torch.log(multilabels)
        self.cml_loss.init_centers(log_multilabels, views)
        self.logger.print_log('initializing centers done.')
        self.mdl_loss.init_threshold(pairwise_agreements)
        self.logger.print_log('initializing threshold done.')
    def train_epoch(self, source_loader, target_loader, epoch):
        self.lr_scheduler.step()
        if not self.cml_loss.initialized or not self.mdl_loss.initialized:
            self.init_losses(target_loader)
        batch_time_meter = AverageMeter()
        stats = ('loss_source', 'loss_st', 'loss_ml', 'loss_target', 'loss_total')
        meters_trn = {stat: AverageMeter() for stat in stats}
        self.train()

        end = time.time()
        target_iter = iter(target_loader)
        for i, source_tuple in enumerate(source_loader):
            imgs = source_tuple[0].cuda()
            labels = source_tuple[1].cuda()

            try:
                target_tuple = next(target_iter)
            except StopIteration:
                target_iter = iter(target_loader)
                target_tuple = next(target_iter)
            imgs_target = target_tuple[0].cuda()
            labels_target = target_tuple[1].cuda()
            views_target = target_tuple[2].cuda()
            idx_target = target_tuple[3]

            features, similarity, _ = self.net(imgs)
            features_target, similarity_target, _ = self.net(imgs_target)
            # features: bx2048, similarity: bxclass
            scores = similarity * self.args.scala_ce
            loss_source = self.al_loss(scores, labels) # 公式7，同时训练 agent 和 f()
            agents = self.net.module.fc.weight.renorm(2, 0, 1e-5).mul(1e5)
            # features: bx2048, agents: classx2048, labels: bx1, similarity: bxclass
            loss_st = self.rj_loss(features, agents.detach(), labels, similarity.detach(), features_target, similarity_target.detach())
            multilabels = F.softmax(features_target.mm(agents.detach().t_()*self.args.scala_ce), dim=1)
            loss_ml = self.cml_loss(torch.log(multilabels), views_target)
            if epoch < 1:
                loss_target = torch.Tensor([0]).cuda()
            else:
                multilabels_cpu = multilabels.detach().cpu()
                is_init_batch = self.initialized[idx_target]
                initialized_idx = idx_target[is_init_batch]
                uninitialized_idx = idx_target[~is_init_batch]
                self.multilabel_memory[uninitialized_idx] = multilabels_cpu[~is_init_batch]
                self.initialized[uninitialized_idx] = 1
                self.multilabel_memory[initialized_idx] = 0.9 * self.multilabel_memory[initialized_idx] \
                                                          + 0.1 * multilabels_cpu[is_init_batch]
                loss_target = self.mdl_loss(features_target, self.multilabel_memory[idx_target], labels_target)

            self.optimizer.zero_grad()
            loss_total = loss_target + self.args.lamb_1 * loss_ml + self.args.lamb_2 * \
                         (loss_source + self.args.beta * loss_st)
            loss_total.backward()
            self.optimizer.step()

            for k in stats:
                v = locals()[k]
                meters_trn[k].update(v.item(), self.args.batch_size)

            batch_time_meter.update(time.time() - end)
            freq = self.args.batch_size / batch_time_meter.avg
            end = time.time()
            if i % self.args.print_freq == 0:
                self.logger.print_log('  Iter: [{:03d}/{:03d}]   Freq {:.1f}   '.format(
                    i, len(source_loader), freq) + create_stat_string(meters_trn) + time_string())

        save_checkpoint(self, epoch, os.path.join(self.args.save_path, "checkpoints.pth"))
        return meters_trn 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
# L_CML 公式6
class MultilabelLoss(torch.nn.Module):
    def __init__(self, batch_size, use_std=True):
        super(MultilabelLoss, self).__init__()
        self.use_std = use_std
        self.moment = batch_size / 10000
        self.initialized = False

    def init_centers(self, log_multilabels, views):
        """
        :param log_multilabels: shape=(N, n_class)
        :param views: (N,)
        :return:
        # 用于初始化全局的均值和方差
        """
        univiews = torch.unique(views)
        mean_ml = []
        std_ml = []
        for v in univiews:
            ml_in_v = log_multilabels[views == v]
            mean = ml_in_v.mean(dim=0)
            std = ml_in_v.std(dim=0)
            mean_ml.append(mean)
            std_ml.append(std)
        center_mean = torch.mean(torch.stack(mean_ml), dim=0)
        center_std = torch.mean(torch.stack(std_ml), dim=0)
        self.register_buffer('center_mean', center_mean)
        self.register_buffer('center_std', center_std)
        self.initialized = True

    def _update_centers(self, log_multilabels, views):
        """
        :param log_multilabels: shape=(BS, n_class)
        :param views: shape=(BS,)
        :return:
        """
        univiews = torch.unique(views)
        means = []
        stds = []
        for v in univiews:
            ml_in_v = log_multilabels[views == v]
            if len(ml_in_v) == 1:
                continue
            mean = ml_in_v.mean(dim=0)
            means.append(mean)
            if self.use_std:
                std = ml_in_v.std(dim=0)
                stds.append(std)
        new_mean = torch.mean(torch.stack(means), dim=0)
        self.center_mean = self.center_mean * (1 - self.moment) + new_mean * self.moment
        if self.use_std:
            new_std = torch.mean(torch.stack(stds), dim=0)
            self.center_std = self.center_std * (1 - self.moment) + new_std * self.moment

    def forward(self, log_multilabels, views):
        """
        :param log_multilabels: shape=(BS, n_class)
        :param views: shape=(BS,)
        :return:
        """
        self._update_centers(log_multilabels.detach(), views)

        univiews = torch.unique(views)
        loss_terms = []
        for v in univiews:
            ml_in_v = log_multilabels[views == v]
            if len(ml_in_v) == 1:
                continue
            mean = ml_in_v.mean(dim=0)
            loss_mean = (mean - self.center_mean).pow(2).sum()
            loss_terms.append(loss_mean)
            if self.use_std:
                std = ml_in_v.std(dim=0)
                loss_std = (std - self.center_std).pow(2).sum()
                loss_terms.append(loss_std)
        loss_total = torch.mean(torch.stack(loss_terms))
        return loss_total
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
# L_MDL 公式4
class DiscriminativeLoss(torch.nn.Module):
    def __init__(self, mining_ratio=0.001):
        super(DiscriminativeLoss, self).__init__()
        self.mining_ratio = mining_ratio
        self.register_buffer('n_pos_pairs', torch.Tensor([0]))
        self.register_buffer('rate_TP', torch.Tensor([0]))
        self.moment = 0.1
        self.initialized = False

    def init_threshold(self, pairwise_agreements):
        # Question：论文中还有一个限制条件，f(x_i)f(x_j)>S，代码只考虑了A(y_i, y_j)
        pos = int(len(pairwise_agreements) * self.mining_ratio)
        sorted_agreements = np.sort(pairwise_agreements)
        t = sorted_agreements[-pos]
        self.register_buffer('threshold', torch.Tensor([t]).cuda())
        self.initialized = True

    def forward(self, features, multilabels, labels):
        """
        :param features: shape=(BS, dim)
        :param multilabels: (BS, n_class)
        :param labels: (BS,)
        :return:
        """
        P, N = self._partition_sets(features.detach(), multilabels, labels)
        if P is None:
            pos_exponant = torch.Tensor([1]).cuda()
            num = 0
        else:
            sdist_pos_pairs = []
            for (i, j) in zip(P[0], P[1]):
                sdist_pos_pair = (features[i] - features[j]).pow(2).sum()
                sdist_pos_pairs.append(sdist_pos_pair)
            pos_exponant = torch.exp(- torch.stack(sdist_pos_pairs)).mean()
            num = -torch.log(pos_exponant)
        if N is None:
            neg_exponant = torch.Tensor([0.5]).cuda()
        else:
            sdist_neg_pairs = []
            for (i, j) in zip(N[0], N[1]):
                sdist_neg_pair = (features[i] - features[j]).pow(2).sum()
                sdist_neg_pairs.append(sdist_neg_pair)
            neg_exponant = torch.exp(- torch.stack(sdist_neg_pairs)).mean()
        den = torch.log(pos_exponant + neg_exponant)
        loss = num + den
        return loss

    def _partition_sets(self, features, multilabels, labels):
        """
        partition the batch into confident positive, hard negative and others
        :param features: shape=(BS, dim)
        :param multilabels: shape=(BS, n_class)
        :param labels: shape=(BS,)
        :return:
        P: positive pair set. tuple of 2 np.array i and j.
            i contains smaller indices and j larger indices in the batch.
            if P is None, no positive pair found in this batch.
        N: negative pair set. similar to P, but will never be None.
        """
        f_np = features.cpu().numpy()
        ml_np = multilabels.cpu().numpy()
        p_dist = pdist(f_np)
        p_agree = 1 - pdist(ml_np, 'minkowski', p=1) / 2
        sorting_idx = np.argsort(p_dist)
        n_similar = int(len(p_dist) * self.mining_ratio)
        similar_idx = sorting_idx[:n_similar]
        is_positive = p_agree[similar_idx] > self.threshold.item()
        pos_idx = similar_idx[is_positive]
        neg_idx = similar_idx[~is_positive]
        P = dist_idx_to_pair_idx(len(f_np), pos_idx)
        N = dist_idx_to_pair_idx(len(f_np), neg_idx)
        self._update_threshold(p_agree)
        self._update_buffers(P, labels)
        return P, N

    def _update_threshold(self, pairwise_agreements):
        pos = int(len(pairwise_agreements) * self.mining_ratio)
        sorted_agreements = np.sort(pairwise_agreements)
        t = torch.Tensor([sorted_agreements[-pos]]).cuda()
        self.threshold = self.threshold * (1 - self.moment) + t * self.moment

    def _update_buffers(self, P, labels):
        if P is None:
            self.n_pos_pairs = 0.9 * self.n_pos_pairs
            return 0
        n_pos_pairs = len(P[0])
        count = 0
        for (i, j) in zip(P[0], P[1]):
            count += labels[i] == labels[j]
        rate_TP = float(count) / n_pos_pairs
        self.n_pos_pairs = 0.9 * self.n_pos_pairs + 0.1 * n_pos_pairs
        self.rate_TP = 0.9 * self.rate_TP + 0.1 * rate_TP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# L_RJ 公式 8
# 与公式8略有不同
class JointLoss(torch.nn.Module):
    def __init__(self, margin=1):
        super(JointLoss, self).__init__()
        self.margin = margin
        self.sim_margin = 1 - margin / 2

    def forward(self, features, agents, labels, similarity, features_target, similarity_target):
        """
        :param features: shape=(BS/2, dim)
        :param agents: shape=(n_class, dim)
        :param labels: shape=(BS/2,)
        :param features_target: shape=(BS/2, n_class)
        :return:
        """
        loss_terms = []
        arange = torch.arange(len(agents)).cuda()
        zero = torch.Tensor([0]).cuda()
        for (f, l, s) in zip(features, labels, similarity):
            loss_pos = (f - agents[l]).pow(2).sum() # 公式8的最后一项，a_i-f(z_k)
            loss_terms.append(loss_pos)
            neg_idx = arange != l
            # 从agent中选出与当前图片特征相似度高于阈值，但不是同一类的的agent
            hard_agent_idx = neg_idx & (s > self.sim_margin) # 越相似，值越大
            if torch.any(hard_agent_idx):
                hard_neg_sdist = (f - agents[hard_agent_idx]).pow(2).sum(dim=1)
                loss_neg = torch.max(zero, self.margin - hard_neg_sdist).mean()
                loss_terms.append(loss_neg)
        for (f, s) in zip(features_target, similarity_target):
            hard_agent_idx = s > self.sim_margin
            if torch.any(hard_agent_idx):
                hard_neg_sdist = (f - agents[hard_agent_idx]).pow(2).sum(dim=1)
                loss_neg = torch.max(zero, self.margin - hard_neg_sdist).mean()
                loss_terms.append(loss_neg)
        loss_total = torch.mean(torch.stack(loss_terms))
        return loss_total

根据代码，重新明确两个定义:

  • similarity 指的是图片的 feature1 和 agent 的 feature2 的特征相似性: feature1*feature2
  • multilabels 指的是 similarity.mul(self.args.scala_ce) 再softmax得到的

算了，有些代码还是跑的时候看吧，因为有些更新方式有些看不懂。